control theory
- Khin Zawshwe

- May 31, 2017
- 5 min read

တကယ္ေတါ႔ control system တခုဟါလိုခ်င္တဲ႔ process အေၿခအေန၇ေအါင္ လုပ္ယူတဲ႔ စံနစ္တခုပါ။ အေပၚက Wikipedia Control Theory မွာပါတဲ႔ အထဲက အခ်ိဳ႔ လိုသေလါက္ ေလ႔လါၿကည္႔၇င္
control theory is to control a system, often called the plant, so its output follows a desired control signal, called the reference, which may be a fixed or changing value. To do this a controller is designed, which monitors the output and compares it with the reference. The difference between actual and desired output, called the error signal, is applied as feedback to the input of the system, to bring the actual output closer to the reference.
In open loop control, the control action from the controller is independent of the "process output" (or "controlled process variable"). A good example of this is a central heating boiler controlled only by a timer, so that heat is applied for a constant time, regardless of the temperature of the building. (The control action is the switching on/off of the boiler. The process output is the building temperature).
Classical control theory
In closed loop control, the control action from the controller is dependent on the process output. In the case of the boiler analogy this would include a thermostat to monitor the building temperature, and thereby feed back a signal to ensure the controller maintains the building at the temperature set on the thermostat. A closed loop controller therefore has a feedback loop which ensures the controller exerts a control action to give a process output the same as the "Reference input" or "set point". For this reason, closed loop controllers are also called feedback controllers.
Closed-loop controllers have the following advantages over open-loop controllers:
disturbance rejection (such as hills in the cruise control example above)
guaranteed performance even with model uncertainties, when the model structure does not match perfectly the real process and the model parameters are not exact
unstable processes can be stabilized
reduced sensitivity to parameter variations
improved reference tracking performance
In some systems, closed-loop and open-loop control are used simultaneously. In such systems, the open-loop control is termed feedforward and serves to further improve reference tracking performance.
A common closed-loop controller architecture is the PID controller.


အေပၚက PID Control ပံု ။ ဟိုးအေပၚက closed loop controller ပံု( feed back က negative feedback)
Linear and nonlinear control theory
The field of control theory can be divided into two branches:
Linear control theory – This applies to systems made of devices which obey the superposition principle, which means roughly that the output is proportional to the input. They are governed by linear differential equations. A major subclass is systems which in addition have parameters which do not change with time, called linear time invariant (LTI) systems. These systems are amenable (ထိန္းေက်ာ္င္းနုိင္ေသါ) to powerful frequency domain mathematical techniques of great generality, such as the Laplace transform, Fourier transform, Z transform, Bode plot, root locus, and Nyquist stability criterion. These lead to a description of the system using terms like bandwidth, frequency response, eigenvalues, gain, resonant frequencies, poles, and zeros, which give solutions for system response and design techniques for most systems of interest.
Linear control theory ကို laplace transform ေတြ. linear differential equations ေတြနဲ႔ ေၿဖ၇ွင္းနိုင္တယ္။ ဒါေပမဲ႔ တကယ္႔ေလါက မွာ linear control theory က အၿပည္႔ မမွန္ဘူး။ ဥပမါ - သေဘါၤ ေပၚသက္ေ၇ာက္ေနတဲ႔ သဘါ၀ပတ္၀န္းက်င္က linear control theory ကိုမလိုက္နာဘူး။ ဒါေၿကာင္႔ အ၇င္ steering gear စံနစ္ကို linear control theory ၿဖစ္တဲ႔ PID နဲ႔ထိန္း၇င္ သေဘါၤက ZIGZAG သြါးေနလို႔ ဆီပိုစါးတယ္လို႔ ေစါဒက တတ္ၿကတယ္။ ဒါေၿကာင္႔ ေနာက္ပိုင္း ADAPTIVE CONTROL ေတြသံုးလါၿကတါေပါ႔။
Nonlinear control theory – This covers a wider class of systems that do not obey the superposition principle, and applies to more real-world systems, because all real control systems are nonlinear. These systems are often governed by nonlinear differential equations. The few mathematical techniques which have been developed to handle them are more difficult and much less general, often applying only to narrow categories of systems. These include limit cycle theory, Poincaré maps, Lyapunov stability theorem, and describing functions. Nonlinear systems are often analyzed using numerical methods on computers, for example by simulating their operation using a simulation language. If only solutions near a stable point are of interest, nonlinear systems can often be linearized by approximating them by a linear system using perturbation theory, and linear techniques can be used.
အဲလို Nonlinear control theory အတြက္ nonlinear differential equation ေတြ၇ိွသတဲ႔။ Poincaré maps, Lyapunov stability theorem ေတြဆိုဘဲ၊
အသံုးမ်ားတါကေတါ႔ nonlinear ကို linear လုပ္ပစ္ၿပီး linear control theory နဲ႔ control လုပ္တါပါဘဲ။
List of the main control techniques
Adaptive control uses on-line identification of the process parameters, or modification of controller gains, thereby obtaining strong robustness properties. Adaptive controls were applied for the first time in the aerospace industry in the 1950s, and have found particular success in that field.
A hierarchical control system is a type of control system in which a set of devices and governing software is arranged in a hierarchical tree. When the links in the tree are implemented by a computer network, then that hierarchical control system is also a form of networked control system.
Intelligent control uses various AI computing approaches like neural networks, Bayesian probability, fuzzy logic,[11] machine learning, evolutionary computation and genetic algorithms to control a dynamic system.
Optimal control is a particular control technique in which the control signal optimizes a certain "cost index": for example, in the case of a satellite, the jet thrusts needed to bring it to desired trajectory that consume the least amount of fuel. Two optimal control design methods have been widely used in industrial applications, as it has been shown they can guarantee closed-loop stability. These are Model Predictive Control (MPC) and linear-quadratic-Gaussian control (LQG). The first can more explicitly take into account constraints on the signals in the system, which is an important feature in many industrial processes. However, the "optimal control" structure in MPC is only a means to achieve such a result, as it does not optimize a true performance index of the closed-loop control system. Together with PID controllers, MPC systems are the most wi
dely used control technique in process control.
Robust control deals explicitly with uncertainty in its approach to controller design. Controllers designed using robust control methods tend to be able to cope with small differences between the true system and the nominal model used for design.[12] The early methods of Bode and others were fairly robust; the state-space methods invented in the 1960s and 1970s were sometimes found to lack robustness. Examples of modern robust control techniques include H-infinity loop-shaping developed by Duncan McFarlane and Keith Glover of Cambridge University, United Kingdom and Sliding mode control (SMC) developed by Vadim Utkin. Robust methods aim to achieve robust performance and/or stability in the presence of small modeling errors.
Stochastic control deals with control design with uncertainty in the model. In typical stochastic control problems, it is assumed that there exist random noise and disturbances in the model and the controller, and the control design must take into account these random deviations.
Energy-shaping control view the plant and the controller as energy-transformation devices. The control strategy is formulated in terms of interconnection (in a power-preserving manner) in order to achieve a desired behavior.
Self-organized criticality control may be defined as attempts to interfere in the processes by which the self-organized system dissipates energy.
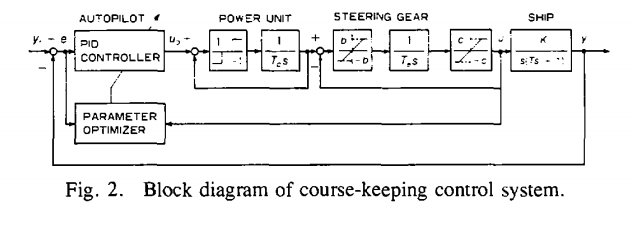
သေဘါၤ၇ဲ႔ ၇ိုး၇ိုး PID STEERING GEAR နဲ႔ ADAPTIVE CONTROL သံုး STEERING GEAR SYSTEM ကြါၿခားမွဳကို ၿပထါးပံု ကေတါ႔
ေအါက္က ပံုက ၇ိုး၇ိုး PID သံုး STEERING GEAR SYSTEM


ေအါက္ကပံုက COURSE KEEPING CONTROL SYSTEM
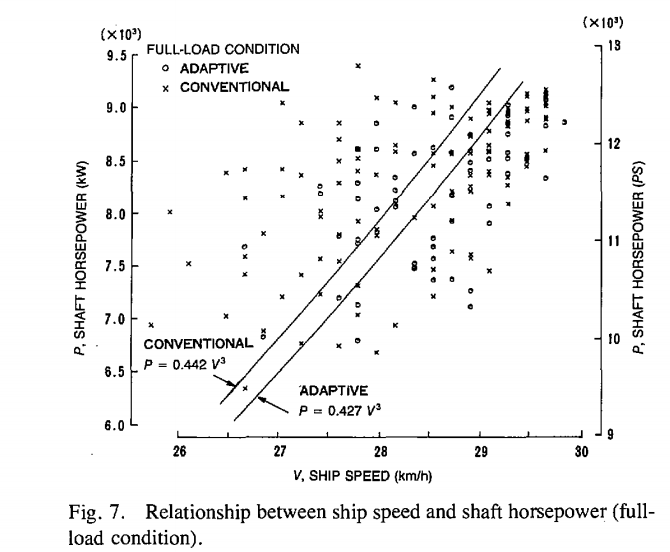
ေအါက္က ပံုက ADAPTIVE က CONVENTIONAL ကြါပံု

အေပၚပံု ADAPTIVE CONTROL နဲ႔ REFERENCE MODEL သံုးထါးတဲ႔ပံု
ေအါက္မွာ အ၇င္သေဘါၤတံုးက သံုးထါးတဲ႔ ADAPTIVE STEERING GEAR အေၿကာင္းၿပထါးပါတယ္။


























































Comments